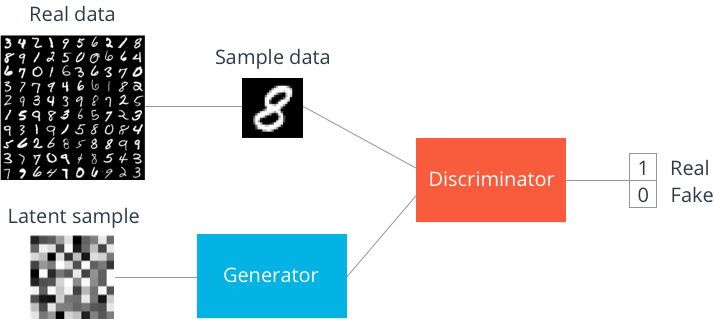
We saw an Intro to GANs and the Theory of Game between Generator and Discriminator in the previous posts. In this post we are going to implement and learn about how to train GANs in PyTorch. We will start with MNIST dataset and in the future posts we will implement different applications of GANs and also my research paper on one of the application of GANs.
So the task is to use the MNIST dataset to generate new MNIST alike data samples with GANs.
Let’s Code GAN
Get the Data
Import all the necessary libraries like Numpy, Matplotlib, torch, torchvision.
import numpy as np
import torch
import matplotlib.pyplot as plt
from torchvision import datasets
import torchvision.transforms as transforms
Now lets get the MNIST data from the torchvision datasets.
transform = transforms.ToTensor()
data = datasets.MNIST(root='data', train=True,
download=True, transform=transform)
data_loader = torch.utils.data.DataLoader(data, batch_size=1024)
The Model
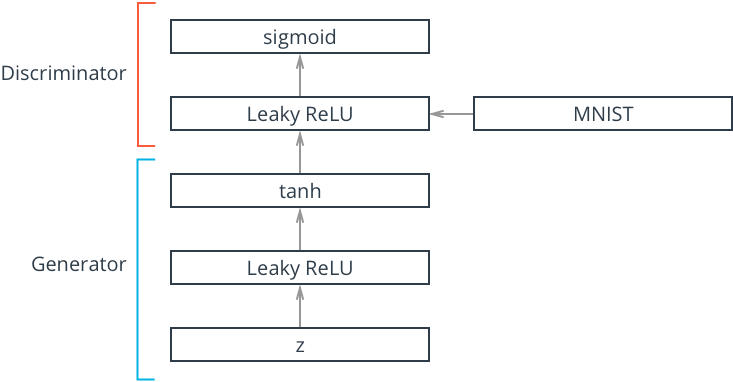
As we have already seen in Theory of Game between Generator and Discriminator, the GAN models generally have 2 networks Discriminator D and Generator G.
We will code both of these network as seperate classes in PyTorch.
Discriminator
The discriminator is a just a classifier , which takes input images and classifies the images as real or fake generated images. So lets make a classifier network in PyTorch.
import torch.nn as nn
import torch.nn.functional as F
class D(nn.Module):
def __init__(self, input_size, hidden_dim, output_size):
super(D, self).__init__()
self.fc1 = nn.Linear(input_size, hidden_dim*4)
self.fc2 = nn.Linear(hidden_dim*4, hidden_dim*2)
self.fc3 = nn.Linear(hidden_dim*2, hidden_dim)
self.fc4 = nn.Linear(hidden_dim, output_size)
self.dropout = nn.Dropout(0.3)
def forward(self, x):
# flatten image
x = x.view(-1, 28*28)
x = F.leaky_relu(self.fc1(x), 0.2)
x = self.dropout(x)
x = F.leaky_relu(self.fc2(x), 0.2)
x = self.dropout(x)
x = F.leaky_relu(self.fc3(x), 0.2)
x = self.dropout(x)
out = F.log_softmax(self.fc4(x))
return out
The D network has 4 linear layers with leaky relu and dropout layers in between.
Here the input size will be 28281 (size of MNIST image)\
hidden dim can be anything of your choice.\
output_size = 2 (real or fake)
I am also adding a log softmax in the end for computation purpose.
Lets make a Discriminator object
D_network = D(28*28*1, 50, 2)
print(D_network)
output :
D(
(fc1): Linear(in_features=784, out_features=200, bias=True)
(fc2): Linear(in_features=200, out_features=100, bias=True)
(fc3): Linear(in_features=100, out_features=50, bias=True)
(fc4): Linear(in_features=50, out_features=2, bias=True)
(dropout): Dropout(p=0.3)
)
Generator
The Generator takes a random vector(z)(also called latent vector) and generates a sample image with a distribution close to the training data distribution. We want to upsample z to an image of size 12828. Tanh was used as activation in the output layer(as used in the original paper) , but feel free to try other activations and check which gives good result.
class G(nn.Module):
def __init__(self, input_size, hidden_dim, output_size):
super(G, self).__init__()
self.fc1 = nn.Linear(input_size, hidden_dim)
self.fc2 = nn.Linear(hidden_dim, hidden_dim*2)
self.fc3 = nn.Linear(hidden_dim*2, hidden_dim*4)
self.fc4 = nn.Linear(hidden_dim*4, output_size)
self.dropout = nn.Dropout(0.3)
def forward(self, x):
x = F.leaky_relu(self.fc1(x), 0.2)
x = self.dropout(x)
x = F.leaky_relu(self.fc2(x), 0.2)
x = self.dropout(x)
x = F.leaky_relu(self.fc3(x), 0.2)
x = self.dropout(x)
out = F.tanh(self.fc4(x))
return out
The G network architecture is same as D’s architecture except now we upsample the z to 28281 size image.
G_network = G(100, 50, 1*28*28)
print(G_network)
G(
(fc1): Linear(in_features=100, out_features=50, bias=True)
(fc2): Linear(in_features=50, out_features=100, bias=True)
(fc3): Linear(in_features=100, out_features=200, bias=True)
(fc4): Linear(in_features=200, out_features=784, bias=True)
(dropout): Dropout(p=0.3)
)
Loss
The discriminator wants the probability of fake images close to 0 and the generator wants the probability of the fake images generated by it to be close to 1.
So we define 2 losses
- Real Loss (loss btw p and 1)
- Fake loss (loss btw p and 0)
p is the probability of image to be real.
-
For Generator : minimize real_loss(p) or p to be closer to 1. ie: fool generator by making realistic images.
-
For Discriminator : minimize real_loss + fake loss. ie: p of real image close to 1 and p of fake image close to 0.
def real_loss(D_out, smooth=False):
batch_size = D_out.size(0)
# label smoothing
if smooth:
# smooth, real labels = 0.9
labels = torch.ones(batch_size)*0.9
else:
labels = torch.ones(batch_size) # real labels = 1
criterion = nn.NLLLoss()
loss = criterion(D_out.squeeze(), labels.long().cuda())
return loss
def fake_loss(D_out):
batch_size = D_out.size(0)
labels = torch.zeros(batch_size) # fake labels = 0
criterion = nn.NLLLoss()
loss = criterion(D_out.squeeze(), labels.long().cuda())
return loss
label smoothing is also done for better convergence.
Training
We will use 2 optimizers
- One for Generator, which optimizes the real_loss of fake images. ie: it tries to make the classification prediction of fake images equal to 1.
- Next is discriminator, which tries to optimize real+fake loss. ie: it tries to make the prediciton of fake images to 0 and real images to 1.
Adjust the no of epochs, latent vector size, optimizer parameters, dimensions etc.
num_epochs = 100
print_every = 400
# train the network
D.train()
G.train()
for epoch in range(num_epochs):
for batch_i, (images, _) in enumerate(train_loader):
batch_size = images.size(0)
## Important rescaling step ##
real_images = images*2 - 1
# rescale input images from [0,1) to [-1, 1)
d_optimizer.zero_grad()
D_real = D(real_images)
d_real_loss = real_loss(D_real, smooth=True)
z = np.random.uniform(-1, 1, size=(batch_size, z_size))
z = torch.from_numpy(z).float()
fake_images = G(z)
D_fake = D(fake_images)
d_fake_loss = fake_loss(D_fake)
d_loss = d_real_loss + d_fake_loss
d_loss.backward()
d_optimizer.step()
g_optimizer.zero_grad()
z = np.random.uniform(-1, 1, size=(batch_size, z_size))
z = torch.from_numpy(z).float()
fake_images = G(z)
D_fake = D(fake_images)
g_loss = real_loss(D_fake)
g_optimizer.step()
if batch_i % print_every == 0:
print('Epoch {:5d}/{:5d}\td_loss: {:6.4f}\tg_loss: {:6.4f}'.format(
epoch+1, num_epochs, d_loss.item(), g_loss.item()))
Epoch 1/ 100 d_loss: 1.3925 g_loss: 0.6747
Epoch 2/ 100 d_loss: 1.2275 g_loss: 0.6837
Epoch 3/ 100 d_loss: 1.0829 g_loss: 0.6959
Epoch 4/ 100 d_loss: 1.0295 g_loss: 0.7128
Epoch 5/ 100 d_loss: 1.0443 g_loss: 0.7358
Epoch 6/ 100 d_loss: 1.0362 g_loss: 0.7625
Epoch 7/ 100 d_loss: 0.9942 g_loss: 0.8000
Epoch 8/ 100 d_loss: 0.9445 g_loss: 0.8455
Epoch 9/ 100 d_loss: 0.9005 g_loss: 0.9073
Epoch 10/ 100 d_loss: 0.8604 g_loss: 0.9908
...
Generate new MNIST Samples
def view_samples(epoch, samples):
fig, axes = plt.subplots(figsize=(7,7), nrows=4, ncols=4, sharey=True, sharex=True)
for ax, img in zip(axes.flatten(), samples[epoch]):
img = img.detach()
ax.xaxis.set_visible(False)
ax.yaxis.set_visible(False)
im = ax.imshow(img.reshape((28,28)), cmap='Greys_r')
sample_size=16
rand_z = np.random.uniform(-1, 1, size=(sample_size, z_size))
rand_z = torch.from_numpy(rand_z).float()
G.eval()
rand_images = G(rand_z)
view_samples(0, [rand_images])
Linear GAN Model does a decent job in generating MNIST images. In next post we will look into DCGAN(Deep Convolutional GAN), to use CNNs for generating new samples.
Check this Awesome Repo on comparing Linear GAN and DCGAN for MNIST. Also this notebook for pytorch implementation of vanilla GAN(Linear).
